Для того чтобы описывать алгоритмы на графах, требуется знать, что такое граф. Граф состоит из вершин и ребер. Вершины графа - объекты любой природы; поскольку их должно быть конечное число, то мы будем обозначать их натуральными числами. Ребра графа соединяют некоторые из его вершин. Если ребра имеют направление, то граф называется ориентированным (орграфом); в противном случае он неориентированный. Если в графе есть ребро C из вершины A в вершину B, то говорят, что ребро C инцидентно вершинам A и B, а также что вершина A смежна с вершиной B.

	а)	б)
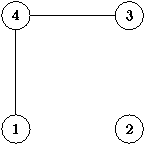
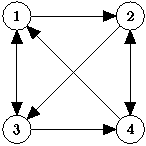
Рис. 1. Примеры графов

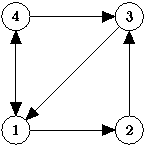
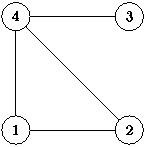
На рис. 1(а) изображен ориентированный граф. Ребра идут из вершины 1 в вершину 2, из 2 в 3, из 3 в 1, из 1 в 4, из 4 в 1, из 4 в 3. На рис. 2(б) изображен неориентированный граф. Ребра соединяют вершины 1 и 2, 1 и 4, 2 и 4, 3 и 4.

Степень вершины - число инцидентных ей ребер. Для орграфа есть входящая степень - число входящих в вершину ребер, и исходящая степень - число исходящих из вершины ребер. Вершина называется четной, если ее степень четна, и нечетной в противном случае. Вершина степени 0 называется изолированной. Путь в графе - последовательность вершин, каждые две соседние из которых смежные. Длина пути - количество вершин в нем минус 1. Если из вершины A в вершину B есть путь, то говорят, что вершина B достижима из вершины A. Путь называется простым, если все вершины в нем различны. Цикл в ориентированном графе - путь длины больше 0, в котором первая и последняя вершины совпадают. Цикл называется простым, если в нем нет совпадающих вершин, кроме первой и последней. В неориентированном графе цикл - путь длины не меньше 3, в котором первая и последняя вершины совпадают. Граф, в котором нет циклов, называется ациклическим. Неориентированный граф называется связным, если из любая его вершина достижима из любой другой. Любой неориентированный граф можно разбить на компоненты связности, т. е. такие непересекающиеся множества вершин, что вершина A достижима из B в том и только в том случае, если эти вершины принадлежат одной компоненте связности.

В графе на рис. 1(а) вершина 1 имеет входящую степень 2, исходящую - 2, вершина 2 - 1/1, 3 - 2/1, 4 - 1/2. В графе на рис. 1(б) вершина 1 имеет степень 2, 2 - 2, 3 - 1, 4 - 3. В графе на рис. 1(а) есть пути (1,2,3,1,4) длины 4, (1,4,3) длины 2, (3,1,4,3) длины 3, причем второй является простым, а третий - простым циклом. В графе на рис. 1(б) есть пути (1,2,4,3), (1,4), (1,4,2,4), причем первые два простые, а третий - цикл. Путь (1,2,1) не является ни простым, ни циклом. Граф справа связный.

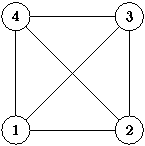
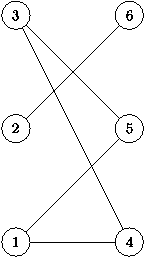
Полный граф - граф, в котором любая вершина смежна любой другой. Двудольный граф - граф, в котором вершины можно разбить на два множества A и B так, что никакие две вершины, принадлежащие одному множеству, не являются смежными. Ациклический неориентированный граф называют лесом, а связный лес называют деревом.

	а)	б)
Рис. 2. Пример полного и двудольного графа.

	а)	б)
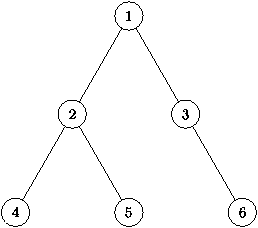
Рис. 3. Пример леса и дерева

В большинстве описанных ниже алгоритмов мы будем считать, что граф задан матрицей смежности, т. е. массивом G размера NxN, где N - число вершин в графе, в котором G[i,j]=true, если есть ребро из i в j, и G[i,j]=false в противном случае. В некоторых случаях мы будем также приводить реализацию алгоритма для графа, представленного в виде списков смежности. Списки смежности - структура, которая каждой вершине сопоставляет список смежных с ней. Мы будем реализовывать списки смежности двумя массивами. Первый - GA - будет для каждой вершины указывать начало ее списка смежности во втором (если GA[i]=0, то из вершины i не исходит ребер), а второй - GB - длины M, где M - число ребер в графе, будет состоять из пар (a,b), где a - номер вершины, которая смежна с той, к которой относится данный элемент списка, а b - номер индекса следующего элемента списка в массиве GB; если b=0, то данный элемент является концом списка.

Некоторые алгоритмы работают на взвешенных графах, у которых каждому ребру сопоставлено число (вес ребра). Чаще всего мы будем рассматривать взвешенные графы с неотрицательными весами. Для этих графов определим матрицу смежности таким образом: G[i,j]=-1, если из i в j нет ребра; иначе G[i,j] равно весу ребра из i в j. Длина пути во взвешенном графе - суммарный вес всех ребер этого пути.

В следующей части этой страницы описаны два способа обхода графов - в глубину и в ширину. Обойти граф означает выписать его вершины в некотором порядке.

Мы рассмотрим два способа обхода неориентированного графа - в глубину и в ширину.

Пусть наш граф из N вершин представлен матрицей смежности G. Заведем массив V из N элементов, в котором на i-м месте будет стоять true, если вершина i была рассмотрена нами ранее, и false в противном случае.

Обход в глубину осуществляется по следующему принципу: сначала посещается вершина 1, затем любая вершина A, соединенная с 1, затем любая еще не посещенная вершина B, соединенная с A и т. д. Когда очередную вершину нельзя будет выбрать, алгоритм будет возвращаться к предыдущей рассмотренной. Таким образом обходятся все компоненты связности графа. Алгоритм обхода в глубину обычно реализуется рекурсивной процедурой:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Boolean;
  V : array [1 .. MaxN] of Boolean;

procedure DFS_Work(A : Integer);
var
  B : Integer;
begin
  V[A] := True;
  Writeln(A);
  for B := 1 to N do
    if G[A,B] and not V[B] then
      DFS_Work(B);
end;

procedure DFS;
var
  A : Integer;
begin
  FillChar(V,sizeof(V),0);
  for A := 1 to N do
    if not V[A] then
      DFS_Work(A);
end;

Например, для графа, изображенного ниже, порядок обхода будет таким: 1,4,2,3,5,6,9,8,7.

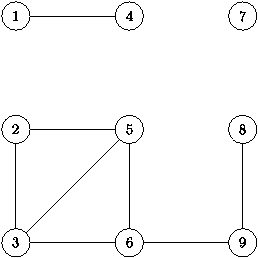Рис. 4. Граф для обхода

Оценим время работы данной реализации алгоритма. Процедура DFS_Work вызывается N раз (по одному разу для каждой вершины), и она делает O(N) действий, не считая рекурсивного вызова; значит, общее время работы O(N^2). Для работы алгоритма требуется O(N) памяти, не считая матрицу смежности (O(N) для хранения массива V и O(N) для хранения стека вызовов процедуры DFS_Work).

Реализация для графа, заданного списками смежности:

const
  MaxN = 100;
  MaxM = 10000;

type
  TConn = record
    A,B : Integer;
  end;

var
  N,M : Integer;
  GA : array [1 .. MaxN] of Integer;
  GB : array [1 .. MaxM] of TConn;
  V : array [1 .. MaxN] of Boolean;

procedure DFS_Work(A : Integer);
var
  B : Integer;
begin
  V[A] := True;
  Add(A);
  B := GA[A];
  while B<>0 do
  begin
    if not V[GB[B].A] then DFS_Work(GB[B].A);
    B := GB[B].B;
  end;
end;

procedure DFS;
var
  A : Integer;
begin
  FillChar(V,sizeof(V),0);
  for A := 1 to N do
    if not V[A] then
      DFS_Work(A);
end;

Данная реализация требует O(M+N) времени и O(N) памяти. (здесь и далее M - число ребер графа).

С помощью обхода в глубину легко найти все вершины, достижимые из данной. Для этого вызовем DFS_Work только для данной вершины. В результате в массиве V значение true будет стоять только для тех вершин, которые достижимы из данной.

Для обхода в ширину нам понадобится очередь. Очередь - это структура данных, над которой можно выполнять четыре операции: очищать ее, добавлять элемент в ее конец, получать ее первый элемент и удалять первый элемент из очереди. Мы реализуем очередь массивом Q из N элементов и двумя счетчиками: Ql и Qr, которые будут указывать положение в массиве соответственно начала и конца очереди. Вначале, когда очередь пуста, Ql=1 и Qr=0. Реализация операций над очередью очевидна.

Мы будем обходить вершины начиная с данной вершины и обойдем только те из них, которые достижимы из нее. Как и при обходе в глубину, заведем массив V из N элементов, но теперь в нем будут записаны целые числа. i-й элемент массива будет равен -1, если i-я вершина еще не была рассмотрена; иначе в i-м элементе будет находиться длина кратчайшего пути от данной до i-й вершины. Обход в ширину очень часто используется для отыскания кратчайших путей из некоторой вершины во все остальные. В этом случае, поскольку сам обход не требуется, требуется убрать из алгоритма строку Writeln(Cur). Порядок обхода вершин в ширину будет таким: сначала данная вершина, потом все вершины, которые с ней смежны, потом все вершины, наикратчайший путь от которых до данной имеет длину 2, и т. д. В конце обхода будут располагаться вершины, наиболее удаленные от данной.

Ход работы алгоритма:
Вначале мы добавляем в очередь первую вершину. Затем, пока очередь не станет пустой, мы рассматриваем первую вершину в очереди, обходим все ранее не обойденные вершины, с ней смежные, и удаляем первую вершину в очереди. При обходе каждой вершины мы добавляем ее в конец очереди.

Реализация алгоритма:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Boolean;
  V : array [1 .. MaxN] of Integer;
  Q : array [1 .. MaxN] of Integer;
  Ql,Qr : Integer;

procedure BFS(A : Integer);
var
  Cur : Integer;
  B : Integer;
begin
  FillChar(V,sizeof(V),255);
  Ql:=1;
  Qr:=1;
  Q[1] := A;
  V[A] := 0;
  while Qr >= Ql do
  begin
    Cur:=Q[Ql];
    Inc(Ql);
    Writeln(Cur);
    for B := 1 to N do
      if G[Cur,B] and (V[B]=-1) then 
        begin
          V[B]:=V[Cur]+1;
          Inc(Qr);
          Q[Qr]:=B;
        end;
  end;
end;

Если запустить BFS(5) для графа с рис. 4, то порядок обхода будет 5,2,3,6,9,8, а в массиве V для вершин 1-9 соответственно будут значения -1,1,1,-1,0,1,-1,3,2.

Оценим время работы алгоритма обхода в ширину. Главный цикл выполняется не более чем N раз (каждая итерация соответствует 1 элементу очереди, и каждая вершина бывает в очереди не более 1 раза), и время выполнения каждой его итерации O(N); значит, общее время работы O(N^2), как и для обхода в глубину; для хранения очереди требуется O(N) памяти. При реализации графа списками смежности алгоритм требует O(M+N) времени.

Рассмотрим орграф из N вершин, не имеющий циклов. Введем на его вершинах частичное отношение порядка, а именно: вершина i считается меньше чем вершина j, если в графе есть ребро из i в j. Задача топологической сортировки состоит в том, чтобы построить для данного графа некоторый порядок обхода его вершин, причем меньшая вершина должна стоять в этом порядке позже, чем большая.

Для реализации алгоритма мы несколько изменим обход в глубину. Заметим, что процедура DFS_Work(A) для орграфа посещает все вершины, достижимые из A, то есть большие чем A. После обработки всех соседей A непройденные вершины не могут быть больше ее: они либо были пройдены до вызова DFS_Work(A), либо были пройдены в процессе работы этого вызова. Значит, вершина A больше, чем все оставшиеся, поэтому мы можем добавить ее в порядок топологической сортировки.

Реализация алгоритма:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Boolean;
  V : array [1 .. MaxN] of Boolean;

procedure DFS_Work_Topolog(A : Integer);
var
  B : Integer;
begin
  V[A] := True;
  for B := 1 to N do
    if G[A,B] and not V[B] then
      DFS_Work_Topolog(B);
  Writeln(A);
end;

procedure Topological_Sort;
var
  A : Integer;
begin
  FillChar(V,sizeof(V),0);
  for A := 1 to N do
    if not V[A] then
      DFS_Work_Topolog(A);
end;

Например, для графа, изображенного на рис. 5, данный алгоритм выдаст порядок обхода 5,3,2,6,1,4.

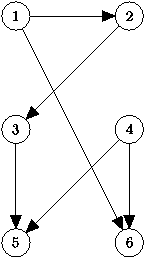Рис. 5. Граф для топологической сортировки

Как и обход в глубину, топологическая сортировка требует O(N^2) времени и O(N) памяти для графа, заданного матрицей смежности, и O(M+N) времени для графа, заданного списками смежности.

Пусть дан неориентированный граф G из N вершин. Требуется покрасить его в два цвета (черный и белый) так, что никакие две вершины одного цвета не будут смежными, либо сказать, что это невозможно.

Для решения этой задачи мы несколько видоизменим алгоритм обхода в глубину. Изменим смысл массива V: V[i]=0, если вершина i еще не была посещена, V[i]=1, если вершина i белого цвета, и V[i]=2, если вершина i черного цвета. Перед каждым рекурсивном вызовом процедуры DFS_Work(b) из процедуры DFS_Work(a) мы будем сравнивать значения V[a] и V[b]; должно выполняться условие V[a]+V[b]=3, иначе раскраска в два цвета невозможна.

Реализация алгоритма:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Boolean;
  V : array [1 .. MaxN] of Byte;

function DFS_Work_BiColor(A : Integer) : Boolean;
var
  B : Integer;
begin
  DFS_Work_BiColor := False;
  Writeln(A);
  for B := 1 to N do
    if G[A,B] then
    begin
      if V[B]=0 then
      begin
        V[B] := 3-V[A];
        if not DFS_Work_BiColor(B) then
          exit;
      end
      else
        if V[A]+V[B]<>3 then
          exit;
    end;
  DFS_Work_BiColor := True;
end;

function BiColor : Boolean;
var
  A : Integer;
begin
  BiColor := False;
  FillChar(V,sizeof(V),0);
  for A := 1 to N do
    if V[A]=0 then
    begin
      V[A] := 1;
      if not DFS_Work_BiColor(A) then
        exit;
    end;
  BiColor := True;
end;

Алгоритм раскраски графа в два цвета требует, как и алгоритм обхода в глубину, O(N^2) времени и O(N) памяти для графа, заданного матрицей смежности, и O(M+N) времени для графа, заданного списками смежности.

Рассмотрим неориентированный связный взвешенный граф с N вершинами. Каркасом в этом графе называется дерево, содержащее все вершины данного графа, причем ребра этого дерева являются также и ребрами графа. Вес каркаса - сумма весов входящих в него ребер. В данном разделе решается следующая задача: найти в графе каркас минимального веса.

Для решения этой задачи есть два алгоритма: Краскала и Прима. Мы рассмотрим только алгоритм Прима.

Рассмотрим взвешенный орграф из N вершин с неотрицательными весами на ребрах. Алгоритм Дейкстры находит в этом графе минимальные длины путей от первой вершины до всех остальных.

Будем записывать результат в массив V длины N, значение которого такое же, как и в алгоритме обхода в ширину. Мы будем делить все вершины графа на помеченные и непомеченные. В начале все вершины непомеченные. Для хранения помеченности вершин используем массив Passed из N элементов, i-й элемент которого будет равен true только если i-я вершина помечена. Кроме того, на каждом шаге алгоритма мы будем считать некоторую вершину графа текущей. Вершина будет помеченной, только если она была на каком-либо шаге текущей.

Каждый шаг алгоритма состоит из двух частей:

1. "Улучшение" вершин. Мы рассматриваем текущую вершину и все вершины, из которых есть в нее ребра. Пусть текущая вершина - Cur, и из нее есть ребро в вершину A. Тогда минимальная длина пути из 1 в Cur равна V[Cur], а длина ребра из Cur в A равна G[Cur,A]; значит, длина минимального пути из 1 в A, на последнем шаге проходящего через Cur, равна V[Cur]+G[Cur,A]; если это число меньше чем V[A] или V[A]=-1, то мы запишем это число в V[A].

2. Выбор новой текущей вершины. Мы выбираем новую текущую вершину как вершину с минимальным значением V из всех непомеченных вершин i, для которых V[i]<>-1; таким образом, новая текущая вершина будет на данный момент самой близкой к 1 из непомеченных.

Алгоритм заканчивает свою работу, когда мы не сможем выбрать текущую вершину.

Реализация алгоритма:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Integer;
  V : array [1 .. MaxN] of Integer;

procedure Djkstra(A : Integer);
var
  B : integer;
  Passed : array [1 .. MaxN] of Boolean;
  Cur : integer;
begin
  fillchar(Passed,sizeof(Passed),0);
  fillchar(V,sizeof(V),255);
  Cur := A;
  V[cur] := 0;
  repeat
    Passed[Cur]:=true;
    for B:=1 to N do
      if (G[Cur,B]<>-1) and ((V[B]=-1) or (V[B]>V[Cur]+G[Cur,B])) then
        V[B]:=V[Cur]+G[Cur,B];
    Cur := 0;
    for B:=1 to N do
      if (not Passed[B]) and (V[B]<>-1) and ((Cur=0) or (V[Cur]>V[B])) then
        Cur := B;
  until Cur=0;
end;

Оценим время работы алгоритма Дейкстры. Алгоритм выполнит не более N шагов (каждый шаг связан с конкретной текущей вершиной), и каждый его шаг требует O(N) операций; значит, время работы алгоритма O(N^2). Очевидно, что алгоритм требует O(N) дополнительной памяти.

Существуют две модификации алгоритма Дейкстры - с двоичной и с фибоначчиевой кучей. Первый из них требует O(M log(N)), а второй - O(N log(N)+M) операций, где M - количество ребер графа. Ввиду некоторой сложности их реализации мы не будем их здесь рассматривать.

Рассмотрим взвешенный орграф G с N вершинами. Алгоритм Флойда находит в нем длину минимальных путей из каждой вершины в каждую.

Реализация алгоритма предельно проста. Мы будем записывать решение в массив V размера NxN: V[i,j] - длина минимального пути из i в j. Вначале V=G. Мы пробегаем все вершины j,i,k и, в том случае если V[i,k] больше чем V[i,j]+V[j,k], то есть пройти из i в k через j быстрее, чем напрямую, мы изменяем значение V[i,k] на V[i,j]+V[j,k].

Реализация алгоритма:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Integer;
  V : array [1 .. MaxN,1 .. MaxN] of Longint;

procedure Floyd;
var
  I,J,K : Integer;
begin
  for I:=1 to N do
  for J:=1 to N do
    V[I,J] := G[I,J];
  for I:=1 to N do
    V[I,I] := 0;
  for J:=1 to N do
  for I:=1 to N do
  for K:=1 to N do
    if (V[I,J]<>-1) and (V[J,K]<>-1) and 
    ((V[I,K]=-1) or (V[I,K]>V[I,J]+V[J,K])) then
      V[I,K] := V[I,J] + V[J,K];
end;

Алгоритм Флойда работает для любых, в том числе и отрицательных, весов ребер графа. Если в графе есть цикл отрицательного веса, то после окончания работы алгоритма для некоторой вершины i будет V[i,i]<0.

Очевидно, что алгоритм Флойда требует O(N^3) операций и O(N^2) дополнительной памяти (для хранения массива V).

Пусть дан орграф G с N вершинами. Эйлеровым циклом в нем называется цикл, в котором каждое ребро графа встречается ровно 1 раз. Можно доказать, что в графе существует эйлеров цикл (граф является эйлеровым) тогда и только тогда, когда граф, во-первых, является связным (не считая изолированных вершин), и, во-вторых, у каждой его вершины входящая степень равна исходящей.

Описанный алгоритм построения эйлеровых циклов уже предполагает, что граф эйлеров. Мы пойдем из любой неизолированной вершины (пусть это вершина 1), и будем идти, добавляя вершины в стек и удаляя ребра, по которым мы проходим, пока мы не сможем пойти из очередной вершины; тогда будем удалять вершины из стека в порядок цикла, пока не встретим вершину, из которой сможем пойти. В результате получим вершины цикла в обратном порядке.

Мы реализуем алгоритм рекурсивной процедурой:

const
  MaxN = 100;

var
  N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Boolean;
  L : array [1 .. MaxN] of Integer;

procedure Euler_Work(A : Integer);
var
  B : Integer;
begin
  B := 1;
  while true do
  begin
    if B<=L[A] then B:=L[A]+1;
    if B>N then break;
    if G[B,A] then
    begin
      L[A] := B;
      Euler_Work(B);
    end;
    Inc(B);
  end;
  Writeln(A);
end;

procedure Euler;
var
  A,B : Integer;
  Found : Boolean;
begin
  Found := false;
  Fillchar(L,sizeof(L),0);
  for A:=1 to N do
  for B:=1 to N do
    if G[A,B] and not Found then
    begin
      Euler_Work(A);
      Found := true;
    end;
end;

Например, для графа, изображенного ниже, порядок будет таким: 1,2,3,4,2,4,1,3,1.

Рис. 6. Эйлеров граф

Время работы данной реализации O(N^2). Алгоритм требует O(M) памяти для хранения стека вызовов процедуры Euler_Work.

Реализация для графа, заданного списками смежности:

const
  MaxN = 100;
  MaxM = 10000;

type
  TConn = record
    A,B : Integer;
  end;

var
  N,M : Integer;
  GA : array [1 .. MaxN] of Integer;
  GB : array [1 .. MaxM] of TConn;
  W : array [1 .. MaxM] of Byte;
  WS : Integer;

procedure Euler_Work(A : Integer);
var
  B : Integer;
begin
  while GA[A]<>0 do
  begin
    B := GA[A];
    GA[A] := GB[B].B;
    Euler_Work(GB[B].A);
  end;
  Inc(WS);
  W[WS] := A;
end;

procedure Euler;
var
  A,B : Integer;
  Found : Boolean;
begin
  Found := false;
  WS := 0;
  for A:=1 to N do
    if (GA[A]<>0) and not Found then
    begin
      Euler_Work(A);
      Found := true;
    end;
  for A:=WS downto 1 do
    Writeln(W[A]);
end;

Данная реализация требует O(M) времени и O(M) памяти.

Рассмотрим неориентированный двудольный граф G из N вершин. Паросочетанием в нем называется некоторый набор ребер этого графа, в котором никакие два ребра не имеют общей вершины. Размер паросочетания - количество в нем ребер. Данный алгоритм находит максимальное паросочетание в графе.

Занумеруем отдельно вершины левой и правой долей графа (доли A и B соответственно). Пусть M и N - размеры долей A и B соответственно. Пусть также G[i,j]=true в том случае, если есть ребро из вершины i доли A в вершину j доли B. Будем записывать решение в массивы ASol и BSol размеров M и N соответственно, где ASol[i]=0, если вершина i доли A не входит в паросочетание; иначе ASol[i] - номер вершины из доли B, с которой соединена i-я вершина в доле A. Аналогично определяется BSol[i].

Будем делить все ребра на две группы: входящие в текущее паросочетание (обратные) и не входящие в него (прямые). Вначале все ребра прямые. Легко проверить, является ли ребро, соединяющее i-ю вершину доли A с j-й вершиной доли B, обратным: это верно в том случае, когда ASol[i]=j (или BSol[j]=i). Назовем чередующимся путем такой путь в графе из некоторой вершины доли A в некоторую вершину доли B, oчто для любых двух последовательных вершин C и D из этого пути верно следующее: если С лежит в доле A, а D - в доле B, то ребро (C,D) прямое; иначе оно обратное. (В силу двудольности графа вершины C и D не могут лежать в одной доле.)

Идея алгоритма следующая: находим в графе чередующиеся пути и разворачиваем их, пока не сможем найти очередной чередующийся путь; в этом случае работа алгоритма завершается и построенное паросочетание (записанное в ASol и BSol) будет максимальным. Разворот пути заключается в следующем: мы меняем статус каждого из его ребер на противоположный, т. е. прямое ребро становится обратным, а обратное - прямым. Заметим, что при этом размер нашего паросочетания увеличивается на единицу. Мы будем перебирать чередующиеся пути, по одному для каждой начальной вершины.

Реализация алгоритма:

const
  MaxN = 100;
  MaxM = MaxN;

var
  M,N : Integer;
  G : array [1 .. MaxN,1 .. MaxN] of Boolean;
  Cur,ACur : Integer;
  ASol,BSol,Prev : array [1 .. MaxN] of Integer;
  Ql,Qr : Integer;
  Q : array [1 .. MaxN*2+1] of Integer;

function PBFS(A : Integer) : Boolean;
var
  B : integer;
  Found : Boolean;
begin
  fillchar(Prev,sizeof(Prev),0);
  Ql := 1;
  Qr := 1;
  Q[1] := A;
  Found := false;
  while (Qr>=Ql) and not Found do
  begin
    Cur := Q[Ql];
    Inc(Ql);
    for B:=1 to N do
      if G[Cur,B] then
      begin
        ACur := B;
        if BSol[ACur]=0 then
        begin
          Found := true;
          break;
        end
        else if Prev[Bsol[ACur]]=0 then
        begin
          Prev[BSol[ACur]]:=Cur;
          inc(Qr);
          Q[Qr]:=BSol[ACur];
        end;
      end;
     end;
     PBFS:=Found;
end;

procedure PMax;
var
  A,B : Integer;
  Tmp : Integer;
begin
  fillchar(ASol,sizeof(ASol),0);
  fillchar(BSol,sizeof(BSol),0);
  for A:=1 to M do
    if PBFS(A) then
      while Cur<>0 do
      begin
        Tmp:=ASol[Cur];
        BSol[ACur]:=Cur;
        ASol[Cur]:=ACur;
        Cur:=Prev[Cur];
        ACur:=Tmp;
      end;
end;

Например, для двудольного графа на рис. 2 справа получим ASol=(1,3,2), BSol=(1,3,2), т. е. в максимальное паросочетание войдут ребра 1-4, 2-6, 3-5.

Процедура PBFS делает O(N^2) действий, и ее вызывают N раз; значит, время работы алгоритма - O(N^3). Требуется O(N) дополнительной памяти.